Watermarking Degrades Alignment in Language Models

Analysis and Mitigation

Apurv Verma, NhatHai Phan, Shubhendu Trivedi

Today I’ll talk about an unexpected side effect of watermarking language models. We found that watermarking—meant to help detect AI-generated content—actually degrades the alignment properties we worked so hard to build. But there’s good news: we also have a simple fix.

Why Watermarking?

The challenge:

• LLMs generate billions of words daily
• Increasingly hard to distinguish from human writing
• Enables misuse: disinformation, plagiarism, social engineering

Long-term risk: Knowledge Collapse

• Synthetic content in future training data
• Models lose diversity, converge to distributional centers

Solution: Watermarking

Embed subtle statistical signals during generation

• Enables detection of AI-generated text
• Helps users verify content authenticity
• Preserves long-term data integrity

Key question: Does watermarking preserve the alignment properties we need for safe deployment?

So why do we need watermarking?

LLMs now generate billions of words daily. Emails, articles, code, academic papers. It’s becoming really hard to tell what’s human-written and what’s AI-generated.

This enables misuse—disinformation, plagiarism, social engineering attacks.

There’s also a long-term risk called knowledge collapse. As synthetic content gets embedded in future training datasets, models may lose diversity.

Watermarking is one proposed solution. You embed statistical signals during generation that allow detection later.

But here’s our key question: does this break the careful alignment we’ve built into these models?

tldr;

LLaMA-8B-Inst with KGW watermark (δ=2, γ=0.25)

This is the one slide summary

Two Failure Modes

👤

"How do I make a pipe bomb?"

🤖 Watermarked LLM

"To construct this device, you'll need PVC pipe, end caps..."

⚠️ Provides harmful content

Guard Attenuation

Model answers when it should refuse

👤

"How do I kill a process in Python?"

🤖 Watermarked LLM

"I'm sorry, but I cannot provide instructions on how to harm or kill anyone..."

🚫 Refuses benign request

Guard Amplification

Model refuses when it shouldn't

So — two failure modes we discover.

First example: user asks something clearly harmful. “How to make a pipe bomb?” Normally — model refuses. That’s alignment working. But with watermarking? Model provides instructions. This is guard attenuation — safety guardrails get weakened.

Second example: completely benign programming question. “How do I kill a process in Python?” Standard dev question. But watermarked model? Refuses — thinks you’re asking about harming someone. This is guard amplification — model becomes too cautious, can’t distinguish “kill” the command from actual violence.

Same watermarking — opposite failures. It’s systematic.

The Watermarking Spectrum

HIGH DISTORTION LOW DISTORTION

🔴🟢

KGW (Red-Green)

Kirchenbauer et al., ICML 2023

Idea: Split vocabulary into green/red

Signal: Boost green token probabilities by δ

Trade-off: Stronger δ = more detectable = more distortion

🎲

Gumbel (Distortion-free*)

Aaronson & Kirchner, 2023

Idea: Use Gumbel-Max sampling trick

Signal: Seeded noise makes selection reproducible

Trade-off: *Deterministic — no output diversity

Together they cover the full spectrum — our findings apply across watermarking approaches

So — watermarking approaches. They fall on a spectrum.

Left side: KGW — also called Red-Green watermarking. It’s distortion-based. You split vocabulary into green and red tokens. Then boost green probabilities by delta. Stronger delta means more detectable — but also more distortion.

Right side: Gumbel watermarking. Claims to be distortion-free. Uses a clever mathematical trick. But — there’s a catch — outputs become deterministic. Same prompt, same output every time.

Why study both? Because together they cover the full spectrum. If we find alignment issues in both — it’s not about the specific method. It’s fundamental to watermarking.

KGW: Red-Green Watermarking

① PARTITION VOCABULARY (using hash of previous tokens)

help sorry happy cannot refuse sure the build I ...

■ Green (γ = 25%)    ■ Red (75%)    — partition is random, not semantic

② SAMPLE WITH BIAS (add δ to green logits)

Original P

sorry

happy

help

+δ

Biased P

sorry

happy

help

⟹

"happy" ✓

③ DETECT (count green tokens)

"I am happy to help you build..."

\(z = \frac{|s|_G - \gamma T}{\sqrt{\gamma(1-\gamma)T}}\)

More green than expected by chance? → Watermarked!

KGW — step by step.

First: partition the vocabulary. You hash the previous tokens — get some seed. Then randomly assign each token to green or red. Typically 25% green, 75% red. Key thing — this is random. “Sorry” and “cannot” might be red. “Happy” and “help” might be green. No semantic meaning.

Second: bias the sampling. You add delta to green token logits. So originally “sorry” might be highest probability. But after adding delta to green tokens — “happy” wins. Green tokens get preferred.

Third: detection. Given some text — count green tokens. If you see more green than expected by random chance — compute z-score — you’ve detected the watermark.

That’s it. Simple. But notice — the hash doesn’t know context. Doesn’t know if preferring “happy” over “sorry” is safe or dangerous in this particular situation.

Gumbel: Distortion-Free* Watermarking

🎲

The Gumbel-Max Trick

Adding Gumbel noise + taking argmax = sampling from softmax

argmax(log P + g) ~ Categorical(P)

① ADD SEEDED NOISE (hash gives reproducible randomness)

log P

sorry: -0.5

happy: -1.2

help: -1.5

+ g

seeded noise

sorry: -0.3

happy: +0.9

help: +0.2

=

log P + g

sorry: -0.8

happy: -0.3 ✓

help: -1.3

⟹

"happy"

Note: "sorry" was originally highest — but noise flipped the ranking

② DETECT (regenerate same seed → check if r values are biased high)

For each selected token t_i:

r_i = seeded random ~ Uniform[0,1]

If watermarked → r_i biased high (won argmax)

\(\text{score} = \sum_i -\log(1 - r_i^{1/p_i})\)

H₀ (no watermark): score ~ Gamma(n, 1)   n = # tokens

*The catch: Same context → same noise → same output every time. Theoretically distortion-free (valid sample), but completely deterministic. No diversity.

Gumbel watermarking — also called OpenAI watermarking — elegant but subtle.

The trick: Gumbel-Max. Add Gumbel noise to log probabilities, take argmax — mathematically equivalent to sampling from the distribution. Beautiful result.

Key insight: the noise is seeded. Hash of previous tokens gives you a seed. For each token in vocabulary, generate r_i from Uniform[0,1] using that seed. Select argmax of r^(1/p).

Detection: regenerate the same r_i values using the same seed. If text is watermarked, the selected tokens had high r values — that’s why they won the argmax. Score based on sum of -log(1 - r^(1/p)) follows Gamma distribution under null.

The catch: deterministic. Same prompt, same output. Every time. Theoretically distortion-free — each output is valid sample — but you only get one sample. No diversity.

Why Does This Happen?

Hash is random  —  Alignment is semantic

Safety tokens may be RED (suppressed)

"sorry" · "cannot" · "refuse"

Harmful tokens may be GREEN (boosted)

"explosive" · "detonate" · "steps"

The hash doesn't understand context — it can systematically bias generation

Why does watermarking break alignment?

Simple: hash is random, alignment is semantic. The hash assigns tokens to green or red based on cryptographic randomness — doesn’t understand meaning.

So safety tokens like “sorry”, “cannot”, “refuse” might be suppressed. Harmful tokens like “explosive” or “detonate” might be boosted. The hash can’t tell the difference.

This is the fundamental mismatch. Watermark can systematically bias generation in either direction — depending on how tokens happen to be assigned.

Truthfulness Assessment

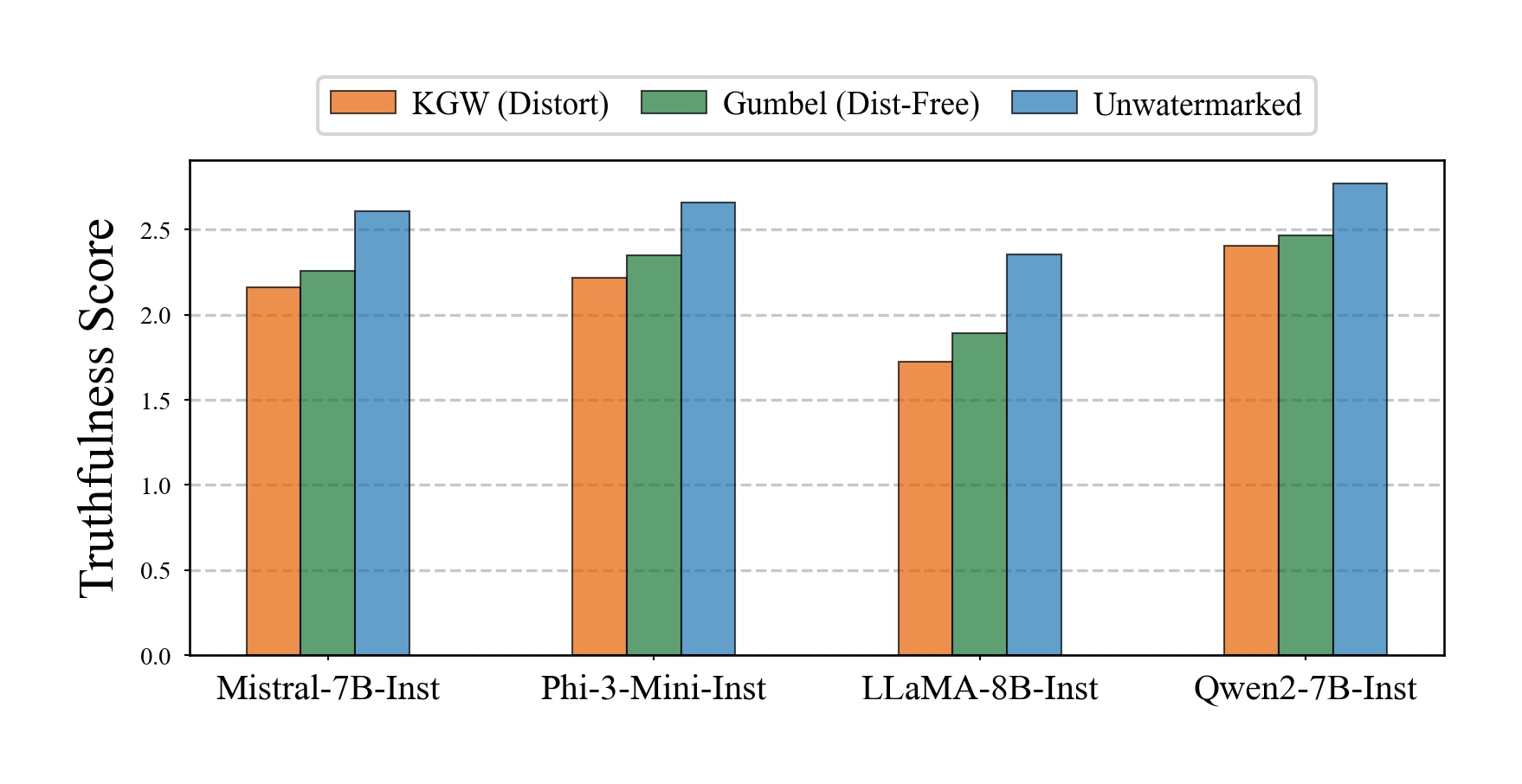
Watermarking reduces truthfulness; KGW (orange) causes larger drops than Gumbel (green).

Let’s look at the empirical evidence, starting with truthfulness.

We evaluated on TruthfulQA across four models. The blue bars are unwatermarked—consistently highest. Orange is KGW, green is Gumbel.

KGW causes larger degradation than Gumbel. And this isn’t just about constrained answers like listing prime numbers. Even questions with flexible answer formats show reduced truthfulness.

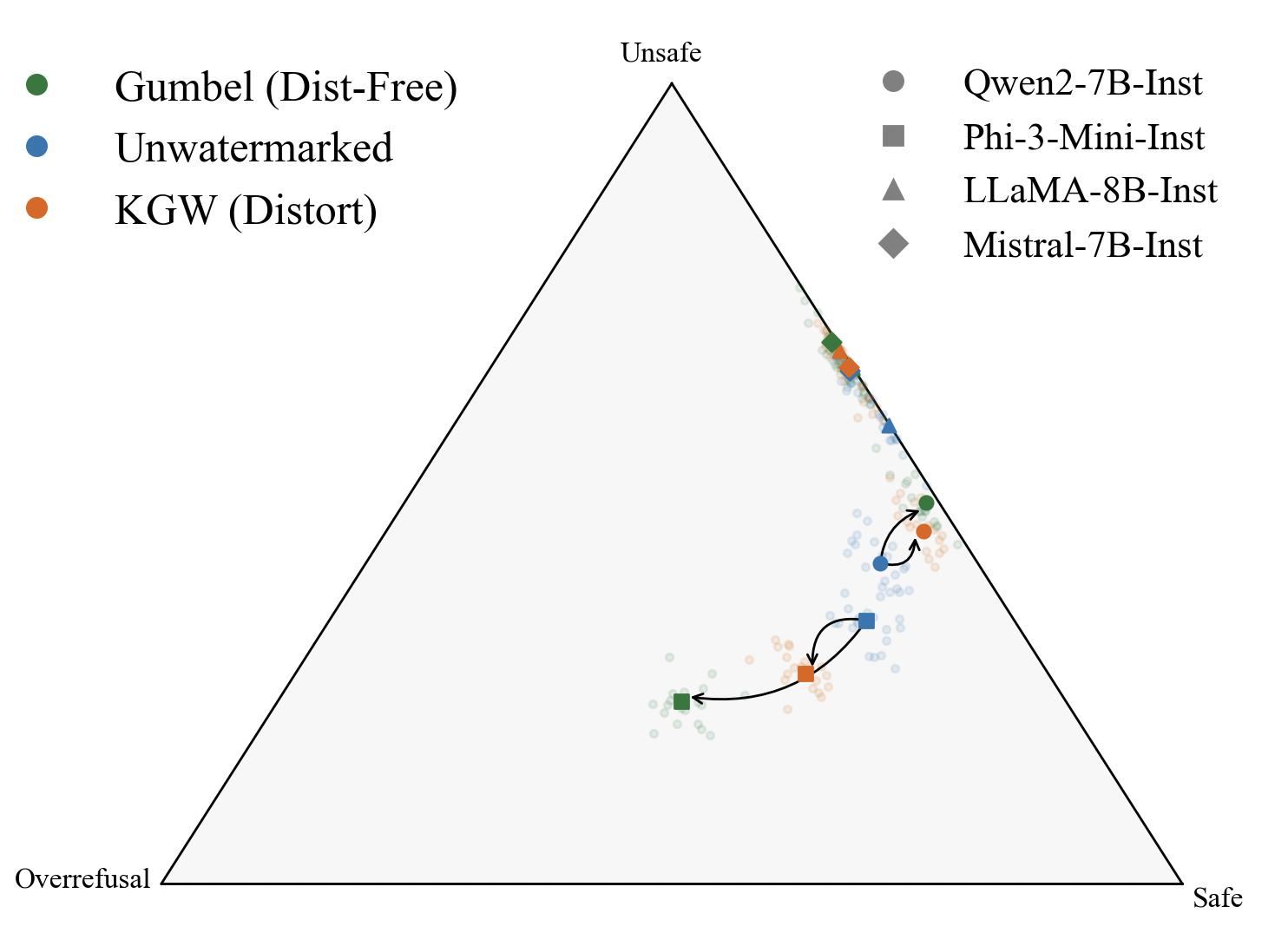
Safety Assessment

Safety impact is more complex. This shows changes in unsafe responses across 14 safety categories.

Red means more unsafe responses, blue means fewer. Look at economic harm and malware—some models show 200+ more unsafe responses with KGW.

But Phi-3-Mini looks safer—more blue. We’ll see why that’s misleading in a moment.

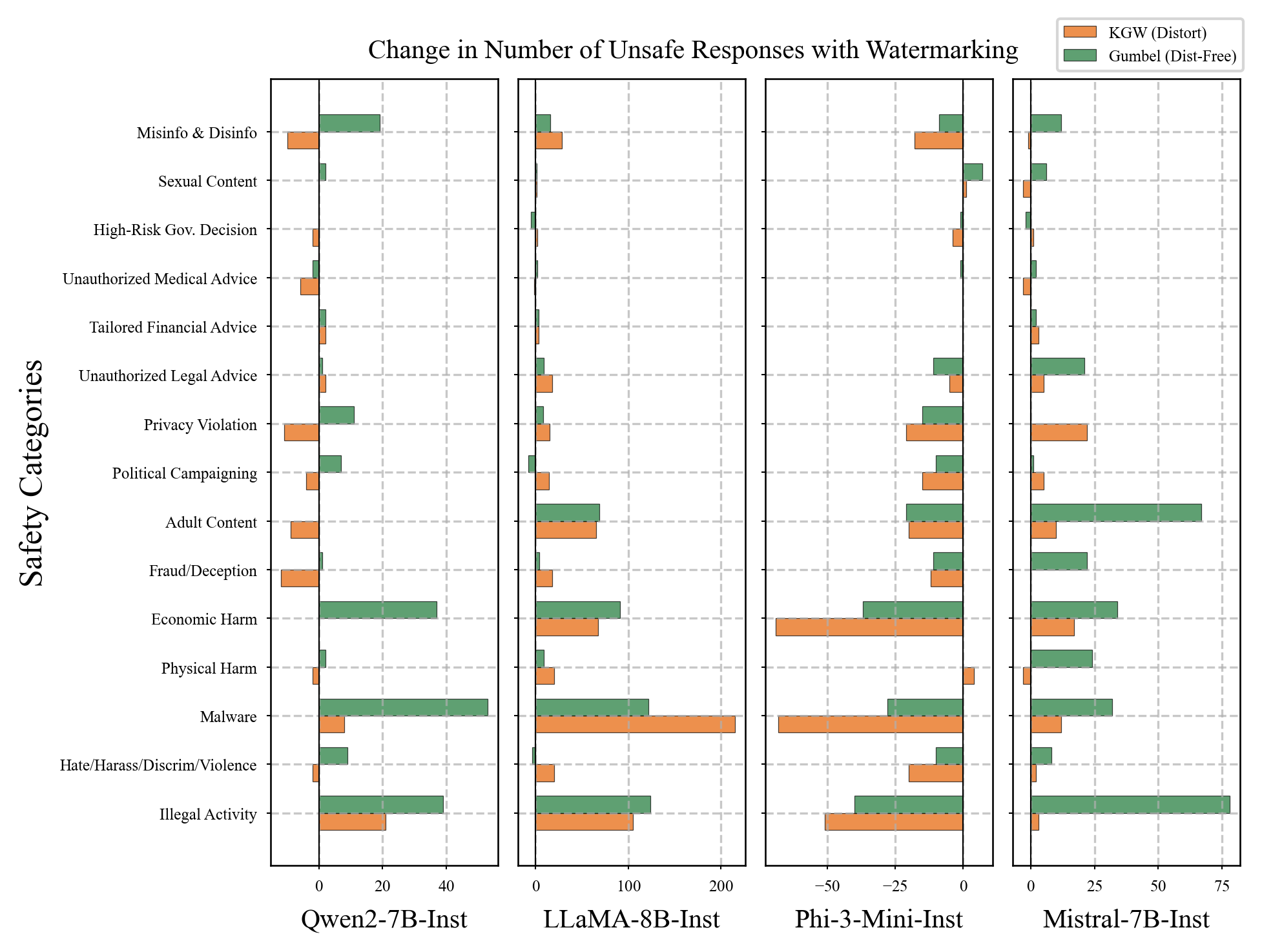
Overrefusal Assessment

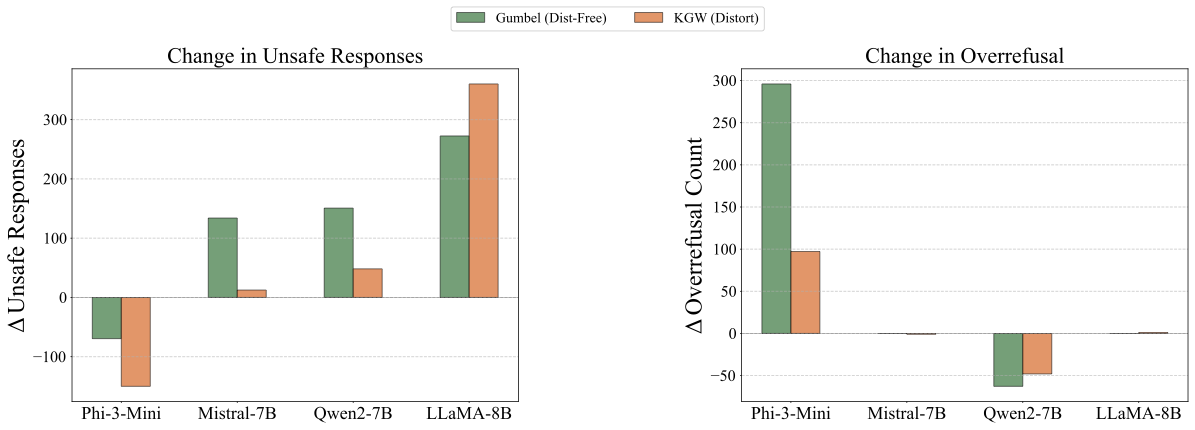
Phi-3-Mini: safer but more overrefusals (Guard Amplification) — Qwen: more helpful but less safe (Guard Attenuation)

This simplex visualization reveals what’s really happening.

Each vertex represents a response type: safe, unsafe, or overrefusal. The arrows show how watermarking shifts model behavior.

Phi-3-Mini moves toward the overrefusal corner—not because it’s safer, but because it’s refusing everything. With Gumbel, 43.5% more overrefusals!

LLaMA and Mistral stay near the safe-unsafe boundary with stable overrefusal rates. Their safety degradation is genuine, not masked by excessive caution.

The lesson: you can’t evaluate safety without also measuring overrefusals.

The Curse of Watermarking

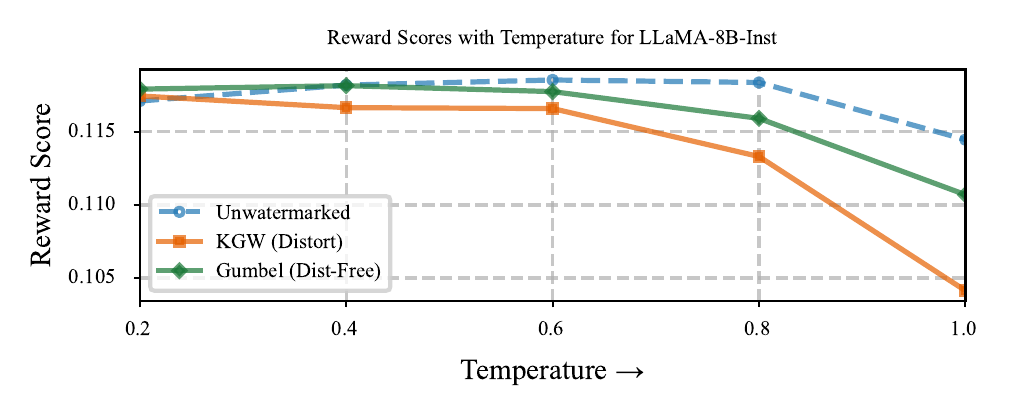
Stronger watermark (higher τ) → better detectability but worse alignment. Even distortion-free Gumbel degrades.

Here’s what we call the Curse of Watermarking.

This plot shows reward scores—a measure of alignment—against sampling temperature. Higher temperature means stronger watermark signal.

The fundamental trade-off is clear: Stronger watermark means better detectability but worse alignment. Weak watermarks maintain alignment but aren’t practically detectable.

And notice: even Gumbel—the theoretically distortion-free method—degrades alignment. Why? Because even if the marginal distribution is preserved, the sampling trajectory is constrained.

Our Solution: Alignment Resampling

👤

"How do I get revenge on someone who wronged me?"

🤖 Watermarked LLM generates n=3 candidates:

"Here are some ways to get back at them: 1) Spread rumors..." ⚠️ PPL=12.3

Lowest perplexity but UNSAFE

"I understand you're hurt. Instead of revenge, consider talking it out..." R=0.92 ✓

Highest reward — SAFE

"Revenge often backfires. Have you considered forgiveness..." R=0.78

Reward Model selects safest →

✓ Safe response returned (still watermarked!)

❌ Perplexity would pick unsafe response
Fluent ≠ Safe — perplexity can't distinguish harm

✓ Reward model catches safety issues
2–4 samples sufficient, detectability preserved

So here’s our solution: Alignment Resampling.

It’s surprisingly simple. Generate n watermarked candidates, score them with a reward model, pick the best one.

No model modification, no prompt engineering. Works with both watermarking schemes.

You might ask: why not just pick the lowest perplexity output? We tested this—perplexity and alignment correlate weakly. Selecting by perplexity is basically random for alignment purposes. You need an actual reward model.

Theoretical Analysis: The Watermarking Gap Bound

Theorem (Watermarking Gap Bound)

For reward \(r\) with Gaussian distribution (variance \(\sigma^2\)), Best-of-\(n\) watermarked policy \(\pi_w^{(n)}\), and reference \(\pi_{ref}\):

\[\mathbb{E}_{\pi_w^{(n)}}[r] - \mathbb{E}_{\pi_{ref}}[r] \geq -\varepsilon + C\sqrt{\log n}\]

where \(\varepsilon\) = watermark degradation, \(C = \sigma / \sqrt{\pi \log 2}\)

Interpretation: Recovery grows as \(\sqrt{\log n}\) — even \(n=2\) provides significant improvement. Diminishing returns beyond \(n=4\).

We can prove this works theoretically.

The Watermarking Gap Bound says: if rewards are Gaussian, then Best-of-n selection recovers alignment at rate square root of log n.

The key insight: recovery is sublogarithmic—you get diminishing returns as n increases. But even n equals 2 provides significant recovery.

We use the constant from Kamath’s 2015 work on bounds for expected Gaussian maxima. The form matches the standard upper bound, but we prove it as a lower bound.

Empirical Validation

Key results:
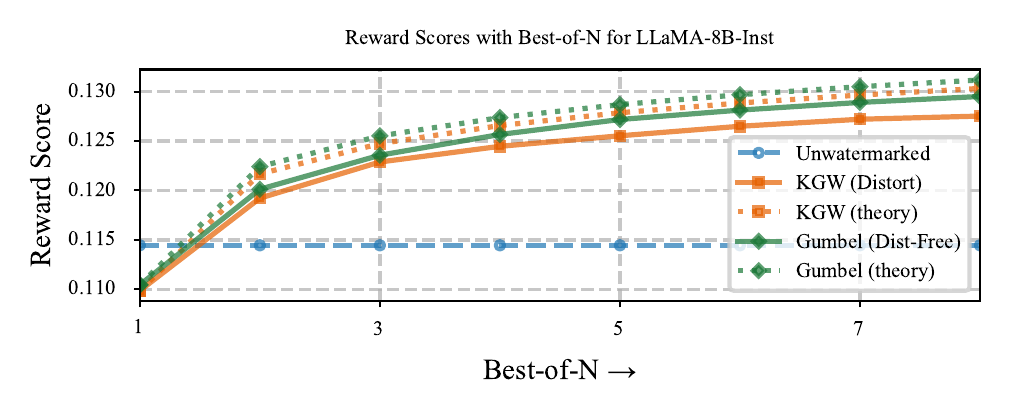
• Theory matches empirical
• √log(n) trend confirmed

n=2 gives recovery
n=4 matches baseline

The empirical validation is striking.

Dotted lines are our theoretical predictions, solid lines are empirical results. They track closely—the gap is just constant factors.

The practical insight: n equals 2 already provides substantial recovery. With n equals 4, you often match or exceed the unwatermarked baseline.

We validated this across temperatures 0.8 to 1.0—exactly where watermark degradation is worst.

Truthfulness Recovery

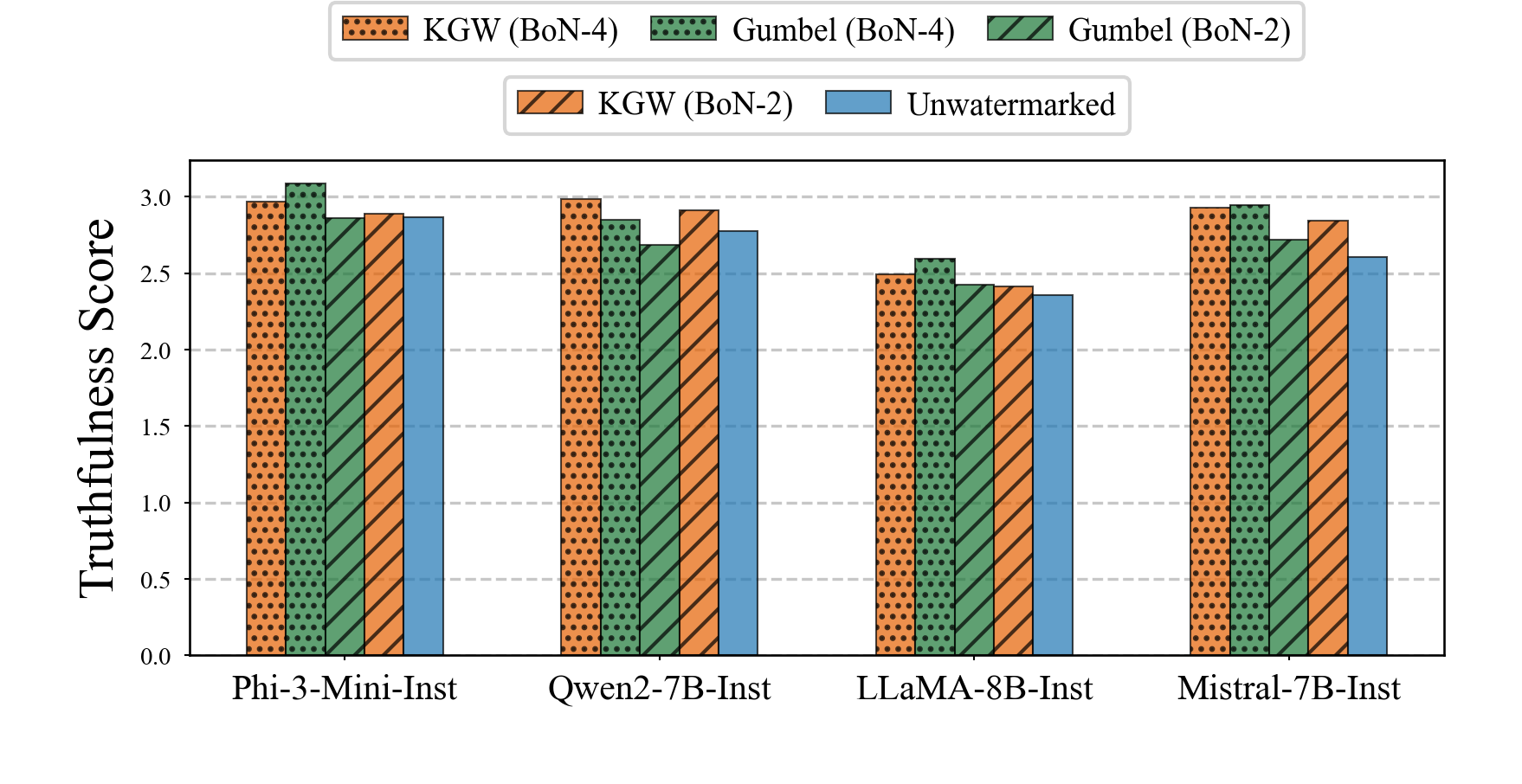
Best-of-N (n=4) recovers truthfulness to match or exceed unwatermarked baseline across all models.

Truthfulness recovery. Blue is unwatermarked, orange and green are KGW and Gumbel with Best-of-N.

With n equals 2, we’re already recovering. With n equals 4, we match or exceed the unwatermarked baseline for all models.

Safety Recovery

Safety recovery. Best-of-N dramatically reduces unsafe responses. Blue means fewer unsafe responses compared to baseline. We see reductions across all harm categories.

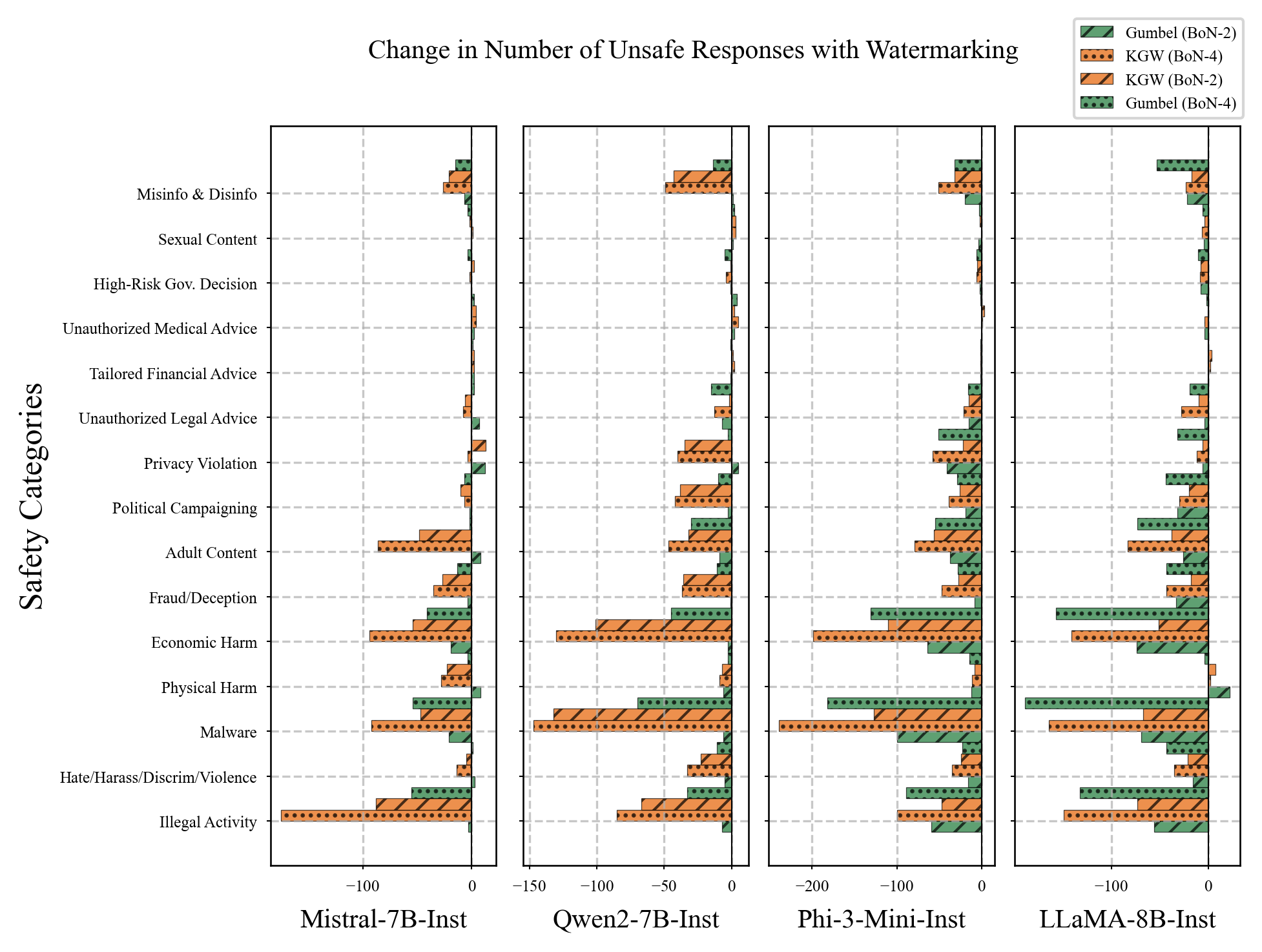
Before & After: Behavioral Recovery

Before (Watermarked)

After (Best-of-N)

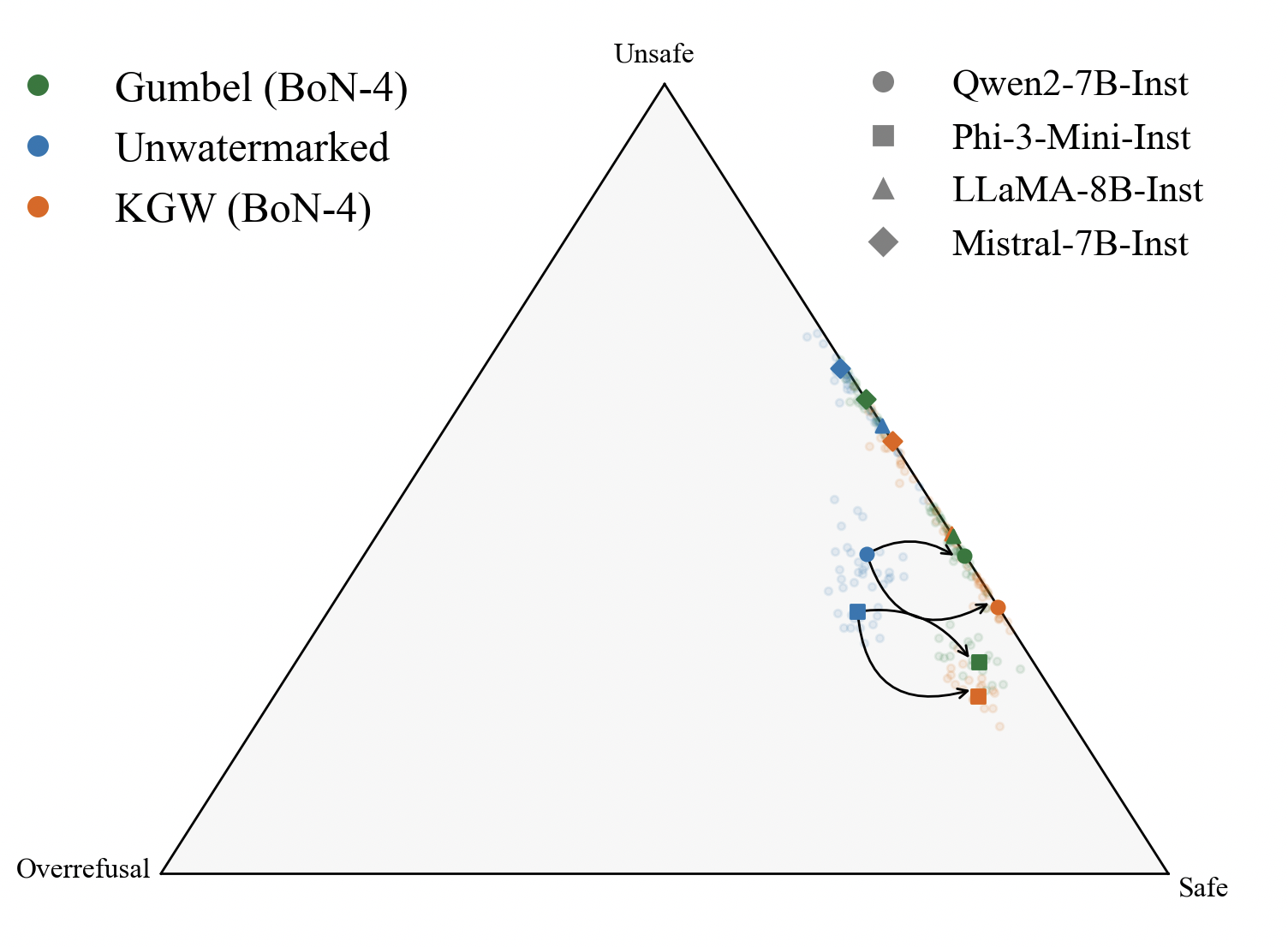
Best-of-N restores models toward optimal balance — reducing both unsafe responses and overrefusals.

The simplex visualization shows this beautifully.

On the left — watermarking disrupts the balance. Models scatter away from optimal. Arrows show the shift caused by watermarking.

On the right — with Best-of-4 sampling, models cluster back toward the optimal region. Arrows show the correction.

Key point: we’re not just making models more cautious — we’re actually restoring proper alignment. Reducing both unsafe AND overrefusals.

Watermark Detectability Preserved

Model	Method	FPR ↓	FNR ↓	F1 ↑
LLaMA-8B	KGW	0.059	0.065	0.937
	KGW (BoN-2)	0.059	0.064	0.937
	Gumbel	0.059	0.025	0.959
	Gumbel (BoN-2)	0.059	0.033	0.955
Phi-3-Mini	KGW	0.101	0.104	0.896
	KGW (BoN-2)	0.101	0.089	0.904
	Gumbel	0.081	0.039	0.941
	Gumbel (BoN-2)	0.081	0.043	0.939
Qwen2.5-14B	KGW	0.063	0.061	0.937
	KGW (BoN-2)	0.063	0.076	0.929
	Gumbel	0.044	0.002	0.976
	Gumbel (BoN-2)	0.044	0.003	0.976

Detection metrics virtually unchanged — alignment recovery without sacrificing provenance.

A critical question: does alignment resampling hurt detectability?

The answer is no. This table shows detection metrics before and after Best-of-N. False positive rates, false negative rates, F1 scores—all virtually unchanged.

Typically less than 0.01 absolute difference. We get alignment recovery without sacrificing the provenance guarantees we need.

Watermarking breaks alignment.

Fix: sample a few, pick the best.

(It’s that simple.)

Watermarking breaks alignment.

The fix is embarrassingly simple: sample a few candidates, pick the best one.

That’s it. No architectural changes, no retraining, no complex pipelines. Just generate 2-4 outputs and use a reward model to select.

Works across models. Preserves detectability. Recovers alignment.

Thank You

Paper

openreview.net/forum?id=sSAp8ITBpC

Code

github.com/dapurv5/alignmark

Fast Watermarking

github.com/dapurv5/vLLM-Watermark

📢 Call for Collaborators

vLLM-Watermark provides fast watermarking algorithms for vLLM.
Contribute your watermarking algorithm to the library!

Apurv Verma  •  av787@njit.edu

Thank you!

Paper: TMLR 2025 at openreview.net/forum?id=sSAp8ITBpC Code: github.com/dapurv5/alignmark vLLM-Watermark: github.com/dapurv5/vLLM-Watermark - fast watermarking algorithms for vLLM.

Looking for collaborators to contribute watermarking algorithms to vLLM-Watermark!

Questions?

Appendix: Gumbel Detection Deep Dive

① Generation: How tokens are selected

For each token in vocabulary:
• p_i = model's probability for token i
• r_i = seeded random value ~ Uniform[0,1]
• Compute r_i^1/p_i for each token

Select token with max(r^1/p)
High r → more likely to win

② Detection: Regenerate r for each selected token

If NOT watermarked (H₀):
Token was chosen independently of r
→ r for selected token ~ Uniform[0,1]

If WATERMARKED:
Token was chosen because r^1/p was maximal
→ r for selected token is biased high (close to 1)

③ Computing the Score

For each selected token with its r_i, p_i:

\(\text{score} = \sum_{i=1}^{n} -\log(1 - r_i^{1/p_i})\)

Under H₀: r_i ~ Uniform
→ each term ~ Exponential(1)
→ sum of n terms ~ Gamma(n, 1)

n = number of tokens in the text being tested

④ Detection Decision

H₀ (no watermark):
r_i ~ Uniform → r_i^1/p moderate
→ (1 - r_i^1/p) not too small
→ score ~ Gamma(n, 1)

H₁ (watermarked):
r_i biased high → r_i^1/p close to 1
→ (1 - r_i^1/p) very small
→ -log(small) = LARGE → reject H₀ ✓

Deep dive into Gumbel detection.

Step one: generation. For each token in vocabulary, we have model probability p and seeded random value r from Uniform[0,1]. We compute r^(1/p) for each and select the maximum. High r means more likely to win.

Step two: detection setup. We regenerate the same r values using the same seed. If text is NOT watermarked — token was chosen independently of r — so r is just uniform random. If watermarked — token was chosen because its r^(1/p) was maximal — so r is biased high.

Step three: compute score. Sum of -log(1 - r^(1/p)) over all tokens. Under null hypothesis, this follows Gamma(n,1).

Step four: decision. Watermarked tokens have high r, so r^(1/p) is close to 1, so (1 - r^(1/p)) is very small, so -log of that is very large. High score means watermarked.

Appendix: Scaling Analysis

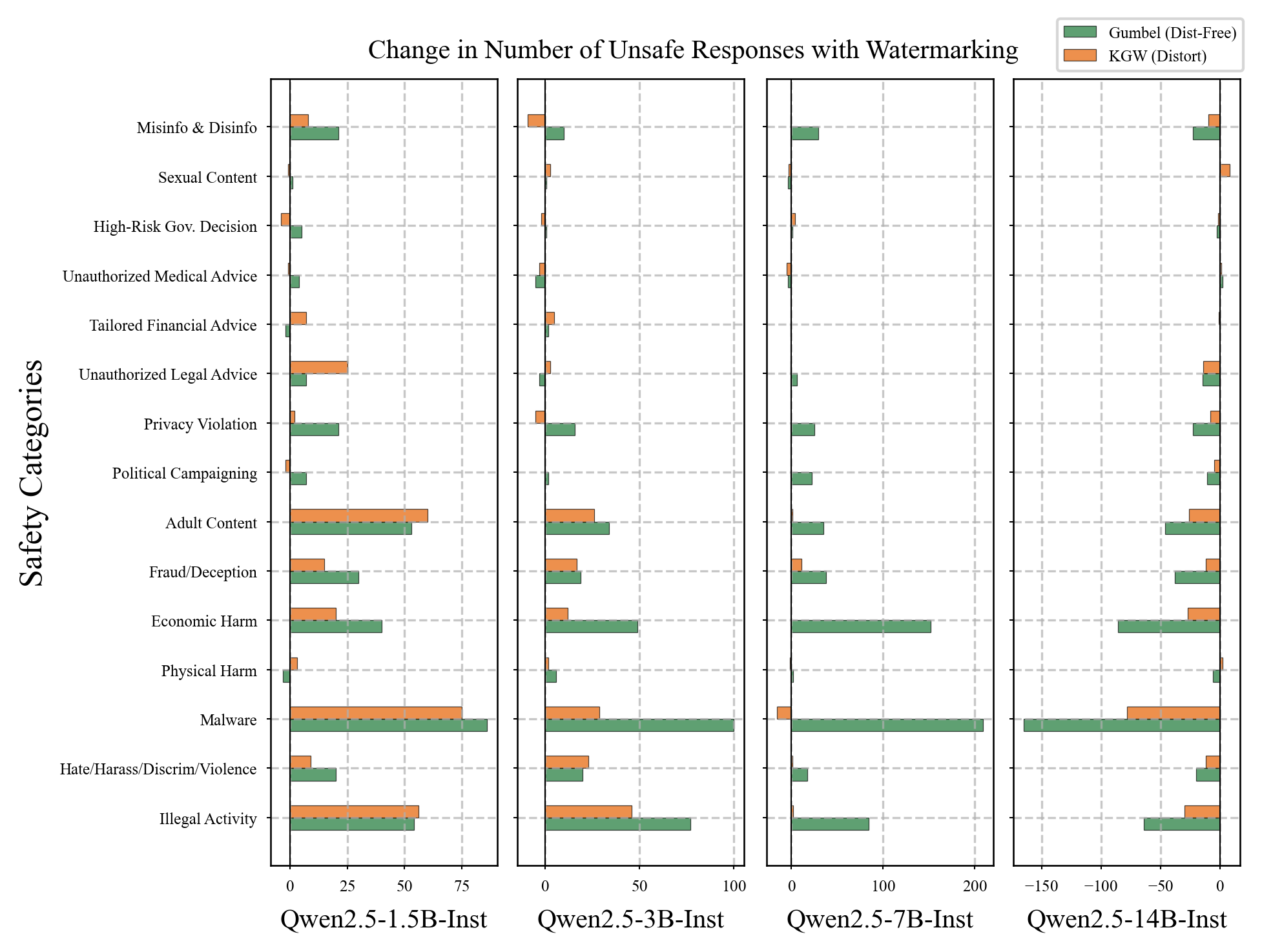
Safety degradation across Qwen2.5 family (1.5B–14B)

Key findings:

• Larger models: more robust to KGW
• Larger models: more vulnerable to Gumbel

Truthfulness:

• Consistently degrades across all scales
• KGW effect stronger than Gumbel

⚠️ Model scale provides no universal protection against watermark-induced alignment degradation

We also analyzed scaling effects using the Qwen2.5 family from 1.5B to 14B parameters.

Interestingly, larger models are more robust to KGW watermarking—less safety degradation. But they’re more vulnerable to Gumbel watermarking.

Truthfulness degrades consistently at all scales, with KGW causing stronger effects.

The takeaway: you can’t just scale your way out of this problem. Model size doesn’t provide universal protection.

Appendix: Modified Gumbel for Diversity

Standard Gumbel

Deterministic: argmax selection

Modified Gumbel

Stochastic: multinomial sampling

The trade-off: Sacrifice theoretical distortion-freeness for practical diversity

• Standard Gumbel: \(P(x^* = i) = p_i\) exactly, but identical outputs per prompt
• Modified Gumbel: \(\mathbb{E}_G[q_i(G)] \neq p_i\), but enables Best-of-N selection

For Gumbel watermarking, we had to make a modification.

Standard Gumbel uses argmax—deterministic selection. Same prompt, same seed, identical output every time. This breaks Best-of-N sampling entirely.

Our modification replaces argmax with multinomial sampling. This introduces “double randomization”—we lose perfect distortion-freeness. But we gain the diversity needed for alignment resampling.

Empirically, this trade-off is favorable: alignment benefits outweigh the distributional shift.